Table of Contents
In the last months, I’m really interested in how database works internally. One of my questions was: “How databases manages indexes? And how they are organized into the storage?”.
I tried to find some resources to understand it, but I didn’t find a good resource that could explain to me in a clear way exactly how it works.
Then, I started to read the Database Internals book, inside it they have some chapters related to B-Tree and how they work. I really recommend this book if you want to learn better how databases work internally.
In this post, I’ll explain to you how B-Trees works as a way I would like to learn about it.
As a way to a better communication through the post, I’ll be calling B-Tree, but I think that it’s important to mention that it will be in notion of B-Tree as an “umbrella” for a given particular family of structures. In case, for our scenario of explanation, I’ll be using the “on-disk B+Tree” as our reference.
If you want to understand better the differences between B-Tree and B+Tree, I recommend you to read this post here.
The structure of a B-Tree
B-Trees are a kind of self-balancing tree data structure that maintains sorted data over a number of levels. It’s composed by nodes that have two specific properties: a key and a value, where the key is the data that will be sorted to let the tree be balanced and handle the binary search through it.
This tree are composed by three specific kind of nodes:
- Root node: The top node of the tree, it’s the only node that doesn’t have a parent node.
- Internal node: The nodes that are between the root node and the leaf nodes. They are used to guide the search through the tree.
- Leaf node: The bottom nodes of the tree, they are the nodes that have the data that we want to search.
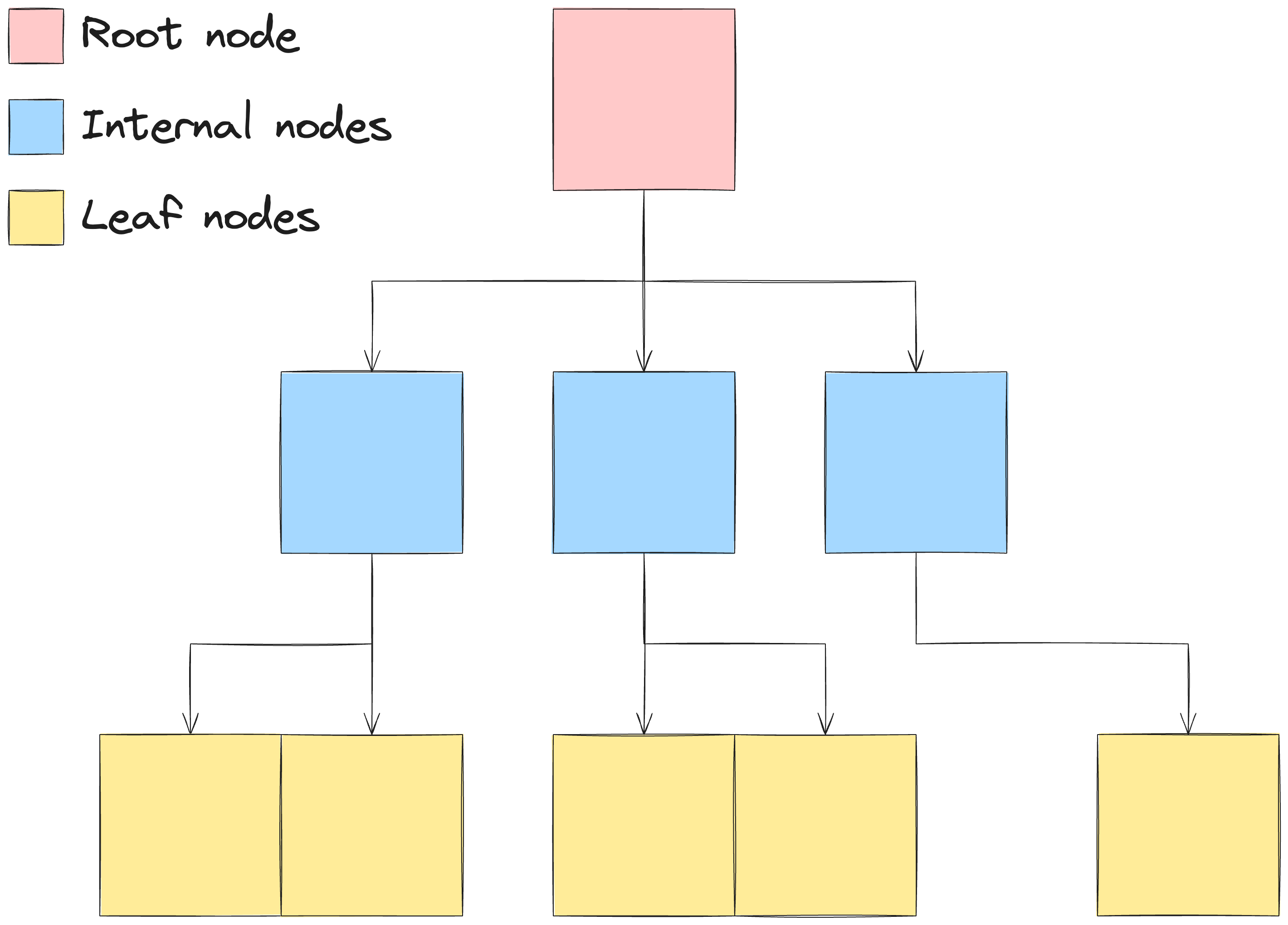
A core property of B-Trees is what we can call it as “fanout”, which is the maximum number of childrens that each non-leaf node can have. The fact that the fanout is how much pointers targeting the children nodes
a node can have, it’s a key property to understand how B-Trees are efficient to search through the data.
In the example of the scenario above, the fanout of the tree is 3. This means that each non-leaf node can have up to 3 children. For a production-ready B-Tree, this fanout number would be much higher, in the order of 100 or more, but for the sake of simplicity, we’ll use 2 as a reference.
The B-Tree Operations
- Explain about insert
- Explain about delete
- Explain about lookup
- Hook to start an explanation about the balancing in both insert/delete
Why we need the balancing?
- Explain how the balancing is important for B-Trees
- Why a balanced tree has more performance than a non-balanced tree
- Explain how each operation has being processed by the rebalancing of a B-Tree
How B-Tree are being structured in storages?
- Give an introduction about the difference between HDDs and SSDs
- Explain about the disk structure containing cells, pages, etc
- Explain how each B-Tree works handling nodes and pages
- Explain about marshalling and how serialized B-Tree data are organized on storage in byte sequence
How Database applies B-Tree structure?
- Explain how database implements B-Trees
- How the indices are build
- How they insert the B-Trees in memory and dump into storage after fulfilled
- How the leaf nodes targets the offset range data for a given record data on the given table
Conclusion
- Just a conclusion lmao
- Write anything that complements the dumped infos